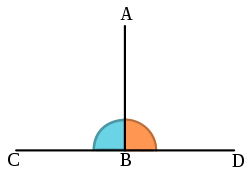Last Year

Hello y'all. Miss being in the same class as you guys :(
I miss Isfeld so much.
TBO 4 lyf.

Range

Range- The positive difference between the largest and smallest values in a data set.

To find range you must: you take the highest number in the data set minus by the lowest number in the set then it will equal the range.

Quadrant

Quadrant

(+,+) quadrant I (-,+) quadrant II (-,-) quadrant III (+,-) quadrant IV

I = 1,  II = 2, III = 3, IV = 4.

Outliers - Values that are too big or too small compared to the other values.
10,11,12,12,14,98
98, would be an outlier.

Range - Positive difference between largest and smallest values

Mode

The most frequently occurring number in a set of data.


27,65,27,97,65,27
27 would be the mode.

Outcome

Outcome- one possible result of a probability experiment

Range

the positive difference between the largest and smallest values in a data set.

Mode

The most frequently occurring number in a set of data.

Outliers

Outliers - Values that are too big or too small compared to the other values.

Quadrant

(+,+) quadrant I (-,+) quadrant II (-,-) quadrant III (+,-) quadrant IV

Range

the positive difference between the largest and smallest values in a data set

Eg.

range of 4,8,5,6,9,1,3,5,8,6 is

1,3,4,5,5,6,6,8,8,9

9-1 = 8

Quadrant

(+,+) quadrant I
(-,+) quadrant II
(-,-) quadrant III
(+,-) quadrant IV

Mean

A measure of central tendency

the sum of a set of values divided by the number of

values in the set

mean of 6,4,8 is

add up all the numbers and divide the results by how many numbers there are

6+4+8=18

18 divide it by 3 = 6

therefor the mean is 6

Mode

The most frequently occurring number in a
set of data

mode and most both have 4 letters

Eg.

mode of 3,5,7,7,9 is 7

mode of 2,2,4,6,6,8,11 is 2 and 6

Median

The middle number in a set
of data after the data have been arranged in order

Eg.

median of 2,5,6,8,9 is 6

median of 1,3,6,8,9,10 is 7

Median Definition

Definition & How to = Outliers

Outliers: Numbers that have small values and numbers that have large values
How to:
ex . 1 , 99 , 99 , 9001 = 1 & 9001
ex . 16 , 4 , 6 , 9 = 16

Definition & How to = Mode

Mode: Most occurring number on a data set

How to find it:

ex...
6 , 5 , 1 , 5 , 7 = 5


Multiples can occur, even no mode at all.

ex...
7 , 1 , 9 , 2 , 8 ≠ No Mode
6 , 9 , 0 , 6 , 9 = 69 or 6 & 9

Height & Base Definitions

Height or 'h': Vertical distance from the top of an object or figure to its base.
Base or 'b': Surface of an object or the line.

Integer / Chips

○ = Positive
● = Negative

|――――――――――――――――――――――――――――――――――――――――|

ex #1...
If Timmy has has 5 cows and somebody stole 3, how many does Timmy have left?
A . ○○○○○ - ●●● = 2

How?

○○○|○○
●●● |
 Left = 2 / ○○
●+○ = 0x3 (x3 because there's 3 negatives)

|―――――――――――――――――――――――――――――――――――――――|

ex #2 in numbers
*** Same Question ***
 In numbers, how?

 5 = ○○○○○ (-3) = ●●●
 5-(-3) = 2 or ○○
|――――――――――――――――――――――――――――――――――――――――|

Base x Height

                                                   A . 24cm²

(Thanks to Gabbey for reminding me for the 'x squared' part ;)

!MATH!

MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
 MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
 MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
 MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
 MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!
 MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!MATH!

Mean,Median,Mode,Range,Outlier

Mean-Add up all values divide by how many values there are

Median- The middle number in a set of ordered values, might be the mean of 2 middle values

Mode- The value that shows up the most

Range- Positive difference between largest and smallest values

Outlier-Values that are too big or too small compared to the other values

Outliers

Outliers- Values that are too big or too small compared to the other values

Mode & Range

Mode-  The value that shows up the most

Range- Positive difference between largest and smallest values

Mean & Median

Mean- Add up all values by how many values there are

Median-  The middle number in a set of ordered values might be the mean of 2 values

How to do a circumference question

Hi i'm back again and today I'm going to show you how to to do a circumference question
lets say the question is d=2 m
1 c=d x 3.14 ( 3.14 is pi)
2 c= 2 x 3.14
c=6.28

How to do two step algebraic equations

here's how you do it lets say the question is  4t-2=10
opposite order of operations
4t-2=10
4t-2+2 = 10 + 2
4t =12
4t/4 = 12/4
t=3

how to add opposite integers

this how to add  opposite integers lets say the integers are 5 and (-10so take what you know about zero pares 5 is smaller value wise than (-10)  so take negative 5 away for now then add 5 + (-5) = 0 so whats left the (-5) that we left alone while we made a zero pare so that's how to add opposite  integers see you latter every body

What is a zero pare

A zero pare is when two two opposite numbers of the same value  are added together to make zero
here is an eg. for you yo look at eg. 8 + (-8)=0 there you that is a zero pare

How to subtract Mixed numbers

This is howto subtract mixed nubers
same thing as befor deal with the fractions first
then the whole numbers          7/10 - 3 1/1 0= 2 6/10
there you have how to subtract mixed numbers

How to add mixed numbers

If you have problems with add mixed numbers watch this
step 1 get rid of the fractions first
step 2 deal with the whole numbers
Now watch this eg. 1 2/3 + 4 2/6
                                 2/3 + 2/6 = 1
                               1 + 1 + 4 = 6
                      
                                 there you have it

How to solve one step aljerbra problems

This is how to solve one step aljerbra problems
step 1 lets say this is the problem a+6=10
step 2 oppisite order of opperations so if it says + you have to - it a + 6 -10 = 4
                                                                                                             A= 4

Outcome

Outcome- one possible result of a probability experiment

favorable outcome- a successful result in a probability experiment

p(outcome) is short for saying probability of something happening
example: P(5) when rolling a six sided die!

Probability
probability- like hood or chance of an event occuring

favorable outcomes dived by possible outcomes

example: flipping a coin      head            1
              calling heads      head or tails   2
probability can be expressed, said or written using fractions,ratios, and percents
example 1/2, 1:2, or 50%

Median- The middle number in a set of data after the data has been arranged in order!!

Example: Find the Median?

1,3,6,8,9,10 = the median is 7

Range

Range- The positive difference between the largest and smallest values in a data set.

how to find the range: you take the highest number in the data set minus by the lowest number in the set then it will equal the range.

Example: 3,5,6,7,10,11,12,16,17
17-3=14
14 is the range!!

Mode
Mode- the most frequently occuring number in a data set.
Example: 3,5,7,7,9 = the mode is 7

Median.

The median is the middle number in a set of data after the data have been arranged in order from least to greatest.

for example- 5,6,7,8,9 the median is 7.

Area of a parallelogram.

base x height.

multiply the base and the height.
*NEVER forget the unit of measurement.

Parallelogram.

-a four sided figure with opposite sides parallel and equal in length .

Parallel Lines.

Parallel lines are lines that are in same plane and never cross or intersect.

probabililty.

probability-likelihood or chance of an event occuring.

we determine this - favourable outcomes divided by possible outcomes.

what is the probability of the spinner landing on green?

Mode.

The mode is the most frequently occuring number in a set of data.

Example-3,6,5,4,3,7 the mode is 3.

MEAN

MEAN-  measure of the central tendency
                    -the sum of a set of values divided by the number of values in the set.

theoretical probability

theoretical probability

formula

formula to find area of circle

integers

Median Definition

Theoretical Probability Definition

Range Definition

Mode Definition

Outlier Definition

BEDMAS review

B.E.D.M.A.S is the order of operations:

B- Brackets
E- Exponents
D- Division
M- Multiplication
A- Addition
S- Subtraction

It all goes in order from Brackets to Subtraction
 

Area of triangle and parallelogram formulas

Area of a triangle:

A= basexheight divided by 2

 Area of a parallelogram:

A= basexheight

Math Exam Review II

 

  
The first one is Perpendicular Bisector- A line that that bisects another line into 2 equal parts
The second one is Angle Bisector- A line that bisects an angle
The third one is Intersecting- 2 lines that meet or cross
The fourth one is Parallel Lines- Lines in the same plane that never meet
The fifth one is Perpendicular- A 90 degree angle

Math Exam Review

Math Exam Review:

 There are three types of Transformations:
1. Translation- Where the shape slides across the coordinate grid.
2. Rotation- When shapes turn around on a fixed point on the coordinate grid.
3. Reflection- When shapes are mirrored across a coordinate grid.

Outlier

Outlier- a value that is much larger or smaller that the other data value
                       - the data set may have more than 1 outlier or zero outliers
Outlier(s) for 24, 32,35,37,38,51 are 24 & 51

Mean

Mean- a measure of the central tendency
                    -the sum of a set of values divided by the number of values in the set.
Mean of 45,76,32
Add up all the numbers and divide the result by how many numbers there are
45+76+32
153/3
Mean= 51

Median

Median- the middle number in a set of data after the data have been arranged in order.
Median of 7,13,15,17,24 is 15
Median of 68,73,82,91,110 is 82

Mode

Mode is the most frequently occurring number in a set of data.
eg.
1,2,2,3 the mode is 2
3,3,4,4,5 the mode is 3 and 4
1,2,3,4 there is no mode
1,1,2,2,3,3 no mode
3,3,4,4,5,5,6 the mode is 3, 4, and 5

Outlier

Outlier is a value that is much larger or smaller than the other data value. The data may have more than one outlier or zero outliers. In other words it is the number that doesn't fit in the set.
eg.
2,96,97,98,99


The outlier is 2.

Range

Range is the positive difference between the largest and smallest values in a a data set.
eg.
6,4,2,5,3,1
1,2,3,4,5,6
6-1=5

Mean and Median

Mean is a measure of central tendency. It is the sum of a set of values divided by the number of values in a set. In other words add up all the numbers and divide the result by how many numbers there are.

eg.
3,5,7
3+5+7=15
15/3=5

Therefor the mean is 5.


Median is also a measure of central tendency. It is  the middle number in a set of data after the data have been arranged in order.


eg.
3,0,1,7,3,2,6
0,1,2,3,3,6,7
The median is 3.


This is how you get the median if you have 2 numbers in the middle:
 -Add the 2 numbers and divide the sum by 2.


 1,2,3,4,5,6

 3+4=7
 7/2=3.5

The median is 3.5

Measures of Central Tendency

The Measures of Tendency is a value that represents the centre of a data set that can be the mean, median, or mode.


Data Set is a group of numbers that you must arrange in order from least to greatest.
eg.
6,6,8,3,2,7,5,9,0,4,6,7,8,3,2

0,2,2,3,3,4,5,6,6,6,7,7,8,8,9

Outlier

A value that is much smaller then the outer data value

The data set may have more then 1 outlier or zero outliers

Eg. Outliers for 1, 67, 68, 67, 64, 65, 100 are 1 and 100

Mean

The sum of a set of values divided by the number of values

Eg. The mean of 6, 4, 8 is 6

Add up all the numbers then divide by how many numbers are in the data set

Mode

The most frequently occurring number in a set of data

Eg. The mode of 3, 5, 5, 6, 7 is 5 because there are 2 5's

Median

Median

The middle number of a set of data after the numbers are arranged in order

Eg. 1, 2, 2, 3, 4, 5, 6, 7, 8

The middle number is 3

Range

Range


The positive difference between the largest and smallest values in a data set


Eg. Range of 1, 7, 7, 8, 8, 9


9 - 1 = 8

Range

Positive difference between largest and smallest values in a data set.

ex: 1,3,4,5,5,6,6,8,8,9
9-1=8

Mode

Frequently occurring number in a set of a data.
 Ex: 2,2,4,6,6,8,11. Mode is 2 and 6.

Median

Middle number in a set of data.  Ex; 1,3,6,8,9,10. Median is 7

Data Set

A data set is a group of numbers that you MUST arrange in order from least to greatest.

Measures of Central Tendency

A value that represents center of a data set.
Can be Mean, Median or Mode.

Outlier

Range

Mean

Mode

Median

outliers

A value that "lies outside" (is much smaller or larger than) most of the other values in a set of data.

range

The difference between the lowest and highest values.

In {4, 6, 9, 3, 7} the lowest value is 3, and the highest is 9, so the range is 9-3 = 6.

mode

The mode is the number that is repeated more often than any other

median

The median is the middle value, so I'll have to rewrite the list in order:

13, 13, 13, 13, 14, 14, 16, 18, 21
There are nine numbers in the list, so the middle one will be the (9 + 1) ÷ 2 = 10 ÷ 2 = 5th number:

13, 13, 13, 13, 14, 14, 16, 18, 21
So the median is 14

mean

The mean is the usual average, so: (13 + 18 + 13 + 14 + 13 + 16 + 14 + 21 + 13) ÷ 9 = 15

Sample Space

Probability

probability

likelihood of an event occurring 

find the median and ouliers 

18 19 79 17 20 12

outliers

small numbers that don't go with bigger numbers 

eg 1 98 99 20

median

 the middle number in a set of data after setting it from least to greatest

mode

the most frequently occurring  number in a set of data

Probability

  -likelihood or the chance of an event occuring
   eg.  
       flipping a coin, rolling a die, etc. 

Line Segment

   -piece of a line with starting and end points
   

Intersecting

Lines in the same plane that meet or cross. 

Height of a Triangle

Height of a Triangle

Here is an example of the height of a triangle:

Height of a Triangle is a perpendicular line from base to opposite angle.

Parallelogram

Heres and example of an parallelogram:

A Parallelogram is a four sided Figure with opposite sides Parallelogram

and equal in length.

Angle Bisector

And Example of An Angle bisector:

(angle ABC)

This is an Angle Bisector.

And angle Bisector is a line that Divides an angle into two equal parts.

-Equal angles are marked with the same angle.

Steps To make an "Angle Bisector"

1. Compass point at the angle vertex make an arc through both arms.

2. Compass point at the vertex of your first arc and make one arm make another arm.

3.Repeat step 2. But from the other arm.

4.Draw line from arc intersecting to angle vertex

Perpendicular Bisector

Perpendicular Bisector  

This is a picture of an perpendicular bisector

A perpendicular Bisector is a line that divides another line segment in half and meets at right angle.

-Equal line segments are hash marks.

How to make a Perpendicular Bisector

1. Open compass to just over half way of a line segment.

2. Sharp point at "A" Make an Ark

3. Sharp Point at "B" make and Ark

4. With ruler join the two intections

Area of a parallelogram

Base x Height, "b x h"

For example:

Area of a triangle

Every triangle is half of a parallelogram. We know the formula to find the area of a parallelogram is base times height. So the formula for the area of a triangle is half the area of a parallelogram. The formula for area of a triangle is base times height divided by 2.


Formula for area of a triangle is: b x h / 2

Here's a link on area of a triangle.

Base and height

Base- Any side of a closed 2 dimensional figure. Common symbol is "b". 
Height- The perpendicular distance from the base to the opposite side. Common symbol is "h". 

Area of Parallelogram

To find the area of a parallelogram you have to to use a formula. That formula is base times height. 

FORMULA: b x h

Base -any side of a closed 2 dimensional figure/shape.

         -common symbol is b.

Height -the perpendicular distance from the base to the opposite side.

            -common symbol is h. 

Here's a link for more information on the area of the parallelogram.

Central Angle

Central Angle- An angle formed by 2 radii with the vertex (2 lines meet or point) at the center of a circle. 

Parallelogram

Parallelogram- a four sided figure with opposite sides parallel and equal in length.

Here's a link on parallelograms. 

Diameter

Perpendicular Bisector

Perpendicular- lines in the same plane that intersect at 90 degree angles.
Bisector- a line that divides another line segment in half and meets at right angle. 
-equal line segments are shown with hash marks.
Perpendicular Bisector- a line that divides another line segment in half and meets at right angle. 

-equal line segments are shown with hash marks.

Here's a link on Perpendicular Bisectors.

Integers

Circumference

Circumference- is the perimeter of a circle. Distance around the circle.

Formula for circumference: 

C=2πr

C=πd

Here's a link about circumference for more information.

Line Segment(s)

Line Segments-
Piece of a line with starting and end points.

Perpendicular

 Perpendicular-
 Lines in the same plane that intersect at 90 degree angles.

 

Area of Parallelogram

ex; base=5 cm, height=3 cm
A= b x h
A= 5 x 3
A= 15 cm 2

Parallel Lines

Parallel Lines-
Lines on the same plane, that never cross or intersect.

ACUTE ANGLE

The measure of an angle with a measure between 0° and 90° or with less than 90°.

More examples in the pictures too.